简介
在学习计量经济学的过程中,许多学生常常会遇到复杂的模型和晦涩的数学推导,感到无从下手。由于缺乏合适的老师或同伴指导,理解这些内容变得更加困难。
AI 助手的出现,为学生们提供了全新的学习方式。通过 AI,学生不仅可以获得模型原理、数学表述和经济学含义的详细讲解,还能根据自己的需求生成 Stata 或 Python 代码、图形和 LaTeX 公式。
更重要的是,AI 能用讲义风格的文字和丰富的代码注释,帮助学生逐步掌握知识点。无论你的基础如何,AI 都可以用通俗易懂的语言,甚至模拟经验丰富的教授,帮助你找到最适合自己的学习路径。
本节的目的是通过 AI 助手,帮助学生理解 Tobit 模型的原理、数学表述和经济学含义。我们将展示如何使用 AI 生成相关内容,并提供实际的代码示例和图形展示。
我主要受到了 Korinek (2023) 的启发。为了解读 Solow 模型的原理 (Chat 50 ),Korinek 向 AI 发送了提示词 Simulate the Solow growth model and plot the results in a four chart.。AI 的解读效果非常好。
模拟 Tobit Model:Python 代码
任务:写一段 {Python} 代码,模拟 Tobit Model 的数据,并酌情绘图。
N = 500;
支持中文字符显示
屏蔽 warning 信息
目的:帮助初学者理解 Tobit Model 的数据生成过程。
风格:讲义风格,核心代码要添加中文注释
import warningsimport numpy as np'ignore' ) # 屏蔽所有 warning 信息 import matplotlib.pyplot as plt'font.sans-serif' ] = ['SimHei' ] # 设置中文字体为黑体 'axes.unicode_minus' ] = False # 正常显示负号 # 设置随机种子,保证结果可复现 42 )# 样本量 = 500 # 生成自变量 X,服从标准正态分布 = np.random.normal(0 , 1 , N)# 设置 Tobit 模型的参数 = 1.0 # 截距 = 2.0 # 斜率 = 1.0 # 残差标准差 # 生成潜在因变量 y*(未截断前的真实值) = beta_0 + beta_1 * X + np.random.normal(0 , sigma, N)# 设置截断点(左截断为0) = np.maximum(y_star, 0 )# 绘图:展示 Tobit 数据的分布 = (10 , 5 ))# 散点图:X 与 y* 的关系 1 , 2 , 1 )= 0.5 , label= 'y*(未截断)' )0 , color= 'red' , linestyle= '--' , label= '截断点' )'X 与 y*(未截断)' )'X' )'y*' )# 散点图:X 与 y 的关系 1 , 2 , 2 )= 0.5 , label= 'y(截断后)' )0 , color= 'red' , linestyle= '--' , label= '截断点' )'X 与 y(截断后)' )'X' )'y' )
模型设定和基本原理
写一段讲义风格的文字,用 LaTeX 公式描述 Tobit Model 的模型设定和基本原理。
然后结合上面的代码和图形解释公式的经济学含义,最好能结合一些容易理解的实例。
Tobit 模型是一种用于处理因变量存在截断(如左截断为 0)的回归模型。其基本思想是:我们观测到的因变量 \(y\) ,是一个潜在的连续变量 \(y^*\) 被某个阈值截断后的结果。
Tobit 模型的数学表述
Tobit 模型可表示为:
\[
\begin{align*}
y_i^* &= \beta_0 + \beta_1 x_i + \varepsilon_i, \quad \varepsilon_i \sim N(0, \sigma^2) \\
y_i &= \begin{cases}
y_i^*, & \text{如果 } y_i^* > 0 \\
0, & \text{如果 } y_i^* \leq 0
\end{cases}
\end{align*}
\]
其中:
\(y_i^*\) :不可观测的潜在因变量(如“理想消费”)\(y_i\) :实际观测到的因变量(如“实际消费”,不能为负)\(x_i\) :自变量\(\beta_0, \beta_1\) :回归系数\(\varepsilon_i\) :正态分布的误差项
经济学含义与实例
以家庭消费为例,\(y_i^*\) 可以理解为家庭的“理想消费金额”,但由于某些家庭可能没有消费(如收入太低),实际观测到的消费 \(y_i\) 就会被截断为 0。
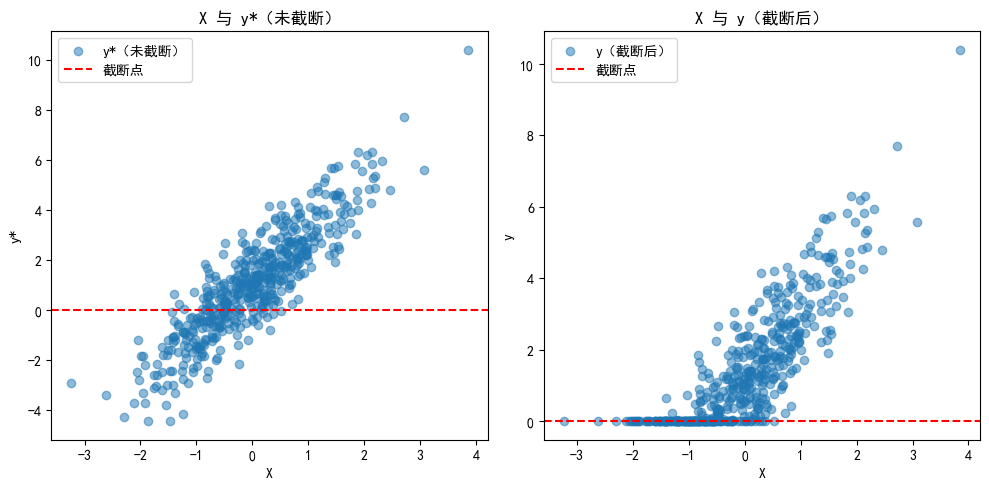
在上面的代码中,我们模拟了 \(N=500\) 个样本,生成了 \(y^*\) 和 \(y\) 。图形左侧展示了 \(X\) 与 \(y^*\) 的关系,可以看到 \(y^*\) 是连续分布的;右侧展示了 \(X\) 与 \(y\) 的关系,所有 \(y^* \leq 0\) 的点都被截断为 0,形成了“堆积”。
这种模型广泛用于:
消费/投资为零的情况(如部分家庭没有购房支出)
信贷申请/批准金额(如部分人未获批贷款)
劳动供给(如部分人未参与劳动市场)
Tobit 模型能有效处理这类“部分观测为零”的数据,避免 OLS 回归的偏误。
Tobit 模型的详细数学推导
其实,仅仅依据上面的内容,你还是无法真正理解 Tobit 模型的数学公式和经济学含义。下面我们将详细推导 Tobit 模型的数学公式,并解释每一步的经济学含义。
我列举了一些提示词要点,你可以酌情选择使用。建议一次性不要给 AI 太多提示词,分步进行更容易获得满意的结果。
写一段讲义风格的文字,详细推导 Tobit 模型的数学公式。包括:
潜在变量 \(y^*\) 的定义
截断后的观测变量 \(y\) 的定义
期望值和条件期望值的推导
Tobit 和 OLS 估计式的关系
Tobit 模型的最大似然估计方法
Tobit 模型边际效应的计算方法和经济含义
潜在变量 \(y^*\) 的定义
Tobit 模型假设存在一个不可观测的潜在连续变量 \(y^*\) ,其生成机制为:
\[
y_i^* = \beta_0 + \beta_1 x_i + \varepsilon_i, \quad \varepsilon_i \sim N(0, \sigma^2)
\]
其中,\(x_i\) 是自变量,\(\beta_0, \beta_1\) 为参数,\(\varepsilon_i\) 为正态分布误差项。
我们实际观测到的因变量 \(y_i\) 受到截断(如左截断为 0),数据生成过程为:
\[
y_i = \begin{cases}
y_i^*, & \text{如果 } y_i^* > 0 \\
0, & \text{如果 } y_i^* \leq 0
\end{cases}
\]
\(y\) 的期望值和条件期望值
Tobit 模型下,\(y_i\) 的条件期望为:
\[
E[y_i|x_i] = P(y_i^* > 0|x_i) \cdot E[y_i^*|y_i^* > 0, x_i]
\]
其体推导如下:
\(P(y_i^* > 0|x_i) = 1 - \Phi\left(-\frac{\beta_0 + \beta_1 x_i}{\sigma}\right)\) ,其中 \(\Phi(\cdot)\) 为标准正态分布函数。\(E[y_i^*|y_i^* > 0, x_i] = \beta_0 + \beta_1 x_i + \sigma \frac{\varphi\left(\frac{\beta_0 + \beta_1 x_i}{\sigma}\right)}{1 - \Phi\left(-\frac{\beta_0 + \beta_1 x_i}{\sigma}\right)}\) ,其中 \(\varphi(\cdot)\) 为标准正态密度函数。
因此:
\[
E[y_i|x_i] = \left[1 - \Phi\left(-\frac{\beta_0 + \beta_1 x_i}{\sigma}\right)\right] \left[\beta_0 + \beta_1 x_i + \sigma \frac{\varphi\left(\frac{\beta_0 + \beta_1 x_i}{\sigma}\right)}{1 - \Phi\left(-\frac{\beta_0 + \beta_1 x_i}{\sigma}\right)}\right]
\]
Tobit 和 OLS 估计式的关系
OLS 直接对 \(y\) 回归会低估 \(\beta_1\) ,因为截断导致大量 \(y=0\) 的观测值,拉低了回归斜率。Tobit 模型通过最大似然法,利用了 \(y=0\) 的概率信息,能更准确估计参数。
模型的最大似然估计方法
Tobit 模型的对数似然函数为,
\[
\ell(\beta_0, \beta_1, \sigma) = \sum_{y_i=0} \log \Phi\left(\frac{-(\beta_0 + \beta_1 x_i)}{\sigma}\right) + \sum_{y_i>0} \log \left[\frac{1}{\sigma} \varphi\left(\frac{y_i - \beta_0 - \beta_1 x_i}{\sigma}\right)\right]
\]
具中,第一项对应被截断的观测,第二项对应未被截断的观测。通过极大化该似然函数,得到参数估计值。
有关 MLE 估计方法介绍,参见如下推文:
Tobit 模型边际效应的计算方法和经济含义
Tobit 模型的系数 \(\beta_1\) 并不是 \(x\) 对 \(y\) 的直接边际效应。\(x\) 对 \(E[y|x]\) 的边际效应为:
\[
\frac{\partial E[y|x]}{\partial x} = \beta_1 \cdot \Phi\left(\frac{\beta_0 + \beta_1 x}{\sigma}\right)
\]
其表示 \(x\) 的影响被截断概率所“缩小”,只有未被截断的部分才体现出 \(x\) 的真实效应。经济学上,这反映了自变量对“实际观测到的因变量”的平均影响。
Tobit 和 OLS 对比
你还可以进步借助 AI 生成 Tobit 和 OLS 模型的估计结果图示,以便说明 OLS 估计可能存在的偏差。
这里用了教育学中一个非常重要的原理:知识迁移。在学习 Tobit 模型过程中,你可以借助对比,将已经掌握的 OLS 模型知识迁移到新的 Tobit 模型上。
目的:编写 Python 代码,图示 Tobit 和 OLS 模型的估计结果,以便说明 OLS 估计可能存在的偏差
风格:讲义风格,核心代码要添加中文注释
代码要求:
要能独立运行,不依赖与此前代码块的设定
支持中文字符显示;屏蔽 warning 信息
后续讨论
按照上述逻辑,你可以不断追问 AI,生成更多内容。这种学习模式与传统的课堂教学和硬啃教科书有很大区别。你完全可以根据自己的基础和需求,调整 AI 的提示词,让其生成最适合你的内容。
比如,你可以使用如下提示词追问:
Tobit 模型如何估计?
如何解释 Tobit 模型的系数含义?边际效应如何计算?
有哪些 Tobit 模型的拓展模型?
在因果推断中,有哪些与 Tobit 模型或者其模型设定思想相关的模型?它们的适用场景是什么?
对于面板数据而言,有哪些主要的 Tobit 模型?
帮我推荐 3-5 篇公司金融领域使用 Tobit 或相关模型进行实证分析的论文。要求:近 10 年发表的;仅限于 JFE, JF, RFS, JFQA, JCF, RFS 等顶级期刊;最好是有数据和代码的。
ChatGPT 对话过程
参考文献
Korinek, A. (2023). Generative AI for Economic Research: Use Cases and Implications for Economists. Journal of Economic Literature, 61(4), 1281–1317. Link (rep), PDF , Appendix , Google .